Çalışmalarımın ağırlıklı kısmı Einstein Görelilik Kuramı üzerinedir. Genellikle klasik kuramda kesin çözümlerle ilgili problemlerle uğraşmaktayım. Bunlar arasında düz uzayzaman fonunda düzlemsel dalgalar, bu dalgaların çarpışması ve bu olayın matematiksel yapısı üzerinde pek çok çalışmam bulunmaktadır. Son zamanlarda herhangi bir boyutta anti-de Sitter fonunda eğriliğin karesi ile inşa edilen tüm teorilerin kesin çözümleri üzerine yoğunlaşmış bulunuyorum. Bu çözümler arasında AdS-düzlemsel ve küresel dalga çözümleri de bulunmaktadır.
İbrahim Güllü, Metin Gürses, Tahsin Çağrı Şişman, Bayram Tekin, AdS Waves as Exact Solutions to Quadratic Gravity, Phys. Rev. D83,084015 (2011)
Bu çözümler Einstein denklemlerinin gravitasyonel düzlemsel dalga içeren kesin çözümlerine yeni örnekler teşkil ederler. Kuramsal olarak var olduğunu bildiğimiz gravitasyonel dalgaların gözlenmesi birçok ulusun ortak çalışması ile başarılmaya çalışılmaktadır. Buna örnek LISA deneyi aşağıdaki şekilde bahsedilmektedir.
Einstein Kuramının en önemli öngörülerinden birisi gravitasyonel dalagaların varlığıdır. Bu dalgalar dolaylı olarak keşfedildi. Birbirleri etrafında hızla dönen çift yıldızlarda gravitasyonel ışımadan dolayı enerji kaybına ve dolayısıyla dönme periyodu azalımına neden olmaktadır. Bu olay PSR B1913+16 çift nötron yıldızı sietminde deneyle gözlenmiştir. Bu gözlemi yapanlar, Taylor ve Hulse 1993 de fizik dalında Nobel Ödülünü kazanmışlardır.
Bu konuda yararlı olabilecek Türkçe kaynak: M. Gürses, Einstein Görelilik Kuramının Önümüzdeki On Yılı: Günce, Sayı 32, Sahife 2-3 (2005)
Şekil 1. 2020 li yıllarda tamamlanıp doğrudan garvitasyonel dalga gözlemi yapması düşünülen LISA deneyi temsili olarak gösterilmektedir. Yeryüzünde yerleşik gözlemevlerinde yapılan deneylerde şimdiye kadar gravitasyonel dalgaya rastlanılmadı ise de LISA deneyi ile bu amaca ulaşılacağına inanılmaktadır. LISA, bir eşkenar üçgenin köşelerinde ve aralarındaki uzaklığın 5 milyon kilometre olduğu üç peykten oluşan bir uzay laboratuvarıdır. Civarından geçen kuvvetli gravitasyonel ışımayı ölçmesi beklenmektedir.
(Wikipedia)
Çalışmalarımın bir kısmı da uygulamalı matematikte yer alır. Matematikte minimal ve Weingarten yüzeyleri hem geometri hem de diferansiyel denklemler konularında oldukça önemli yer tutar. Euler, Lagrange, Meusner, Plateau, Laplace, Poisson ve Willmore bu konuyu günümüze taşıyan önemli matematikçiler arasında yer alırlar.
Minimal yüzeyler, Weingarten yüzeyleri ve onların genellemeleri matematik ve fizikte olduğu kadar diğer disiplinlerde de sıkça görülen geometrik yapılardır. Uygulamalı matematikte bu yüzeyler yaygın çalışılan popüler konulardan biridir. Bu konuyla entegre edilebilen denklemler arasındaki ilişki oldukça ilginç yer tutmaktadır.
Sabun köpüğü, alyuvar kan hücrelerinin yüzeyi gibi kapalı yüzeyleri içeren tüm olaylarda uygulama alanları bulunan bu konuda öğrencilerimle birlikte çeşitli yayınlarım bulunmaktadır.
Entegre edilebilen denklem sistemlerinden kaynaklanan yüzeylere soliton yüzeyleri diyoruz. Bu konuda yararlı olabilecek bir Türkçe kaynak: M. Gürses, Soliton Yüzeyleri, Türk Matematik Derneği Ankara şubesi Etkinliği, 2001
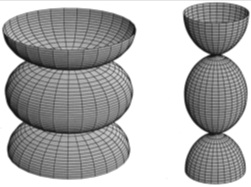
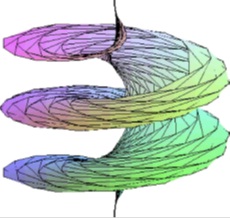
Aşağıda Weingarten ve soliton yüzeylerine birer örnek görmektesiniz.
Şekil 2. Weingarten yüzeyleri
Ö. Ceyhan, A.S. Fokas and M. Gürses, Deformations of Surfaces Associated with Integrable Gauss-Meinardi-Codazzi Equations , Journal of Mathematical Physics , Vol. 41, 2251-2270 (2000).
Şekil 3. Değişik Korteweg de-Vries yüzeylerine bir örnek.
Süleyman Tek, J. Math. Phys. 48, 013505 , 2007